|
Student's Study Guide for Lesson Eleven
by Dr Jamie Love |
|
 and
and  licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.

|
Student's Study Guide for Lesson Eleven
by Dr Jamie Love |

|
The ratios might be slightly "______" (a math term for "off") due to the number of individuals you collected or just "___ ____".
P = smooth seeds crossed with wrinkled seeds
F1 = all smooth seeds (so smooth is ________ and wrinkled is _________)
F2 = 5,474 smooth seeds and 1,850 wrinkled seeds is a ratio of 2.96 : _
Mendel and the Punnett square tell us that we should have a ratio of _ : 1 not 2.96 : 1!
It depends upon how close the ______, observed numbers are from the __________, expected numbers.
Mendel used the chi-square (abbreviated 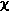 2) test.
2) test.
The chi-square test, or simply the "chi-square", ________ the significance of the data in comparison with what you expect to get. The 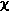 2 only requires that you know the ______ of individuals observed in each category and what numbers you expected them to be.
2 only requires that you know the ______ of individuals observed in each category and what numbers you expected them to be.
In chi-square analysis you compare the number of individuals of a certain phenotype (or ________ else) that you have found in the experiment to the number you ________ to have.
You find the difference between the observed and the expected by simply subtracting one from the other.
Then, you square it (multiply it by ______). That gives you the "squared difference".
Then you ______ the "squared difference" by what you expected in the first place in order to give you a "squared difference per expected" for that group.
Take into account all the different _____ by adding together these "squared differences per expected" values for each class.
The final sum (of the "squared differences per expected") gives you a number called the 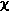 2.
2.
F2 = 5,474 smooth seeds and 1,850 wrinkled seeds for a ratio of ____ : 1
We use the "___ _______" of the data and compare it to the "raw numbers" we expected.
Step 1: calculate the ________ number of each type.
Add together both seed types = a total population of _____ seeds.
Of those 7,324 seeds you expected a _______ of them (1 in 4) to be wrinkled.
So, how many of those 7,324 seeds should be wrinkled?
[______________________________________________________.]
How many smooth seeds should you expect from the total of 7,324 seeds?
[_______________________________________________________________.]
We expected _____ smooth seeds and _____ wrinkled seeds.
Step 2: calculate the "squared differences per ________".
We observed 5,474 smooth seeds but expected 5,493 a DIFFERENCE of __.
Next we ______ THE DIFFERENCE. 19 x 19 (or 192) = 361.
Next we find the SQUARE OF THE DIFFERENCE PER ________ by dividing that number by the total number of smooth seeds we expected to see (5,493). So that is 361/5,493 = _____
Now the next class. We observed 1,850 wrinkled seeds but expected _____. That's a difference of 19. Square the difference to get 361. Divide it by the expected number of ________ seeds (NOT the expected number of ______ seeds - a common mistake) so that is ___/_____ = 0.197
Step 3: congratulate yourself for having got through the ________ part! 
Step 4: ___ up the "squared differences per expected" from all the categories.
0.066 + 0.197 = _____
This experiment (above) has a chi-square equal to 0.263 (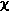 2 = 0.263).
2 = 0.263).
Step 5: _______ our chi-square value to the value in a chi-square significance table and determine if our value is significant.
For our work we want to know if these results pass a significance level of __.
|
Your degrees of freedom are one less than the number of __________ you have to work with.
We have two categories, smooth and wrinkled, so we have one ______ of _______. With one degree of freedom we could be allowed a chi-square as large as ____ and the results would still be considered ___________ to 5%. |
|
We would have to get a chi-square value ____ 3.84 before we would say that our results were so far from a 3 : 1 ratio that we would have to ______ that ratio (and Mendel's explanation of how he got that ratio).
With a 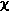 2 = 0.263 there's less than a 5% chance that this 3:1 ratio happened by ________.
2 = 0.263 there's less than a 5% chance that this 3:1 ratio happened by ________.
The Chi-square is a kind of "mathematical judge" of _____________.
Imagine Mendel ________ in this experiment 5,493 smooth seeds and 1,831 wrinkled seeds.
That is an exact 3 : 1 _____.
Looking first at the smooth seeds we would see that the difference between the observed and expected is ____!
When we square zero we still get zero. If we divide zero by the expected value we get ____!
The same happens when we calculate the values for the wrinkled seeds too.
Now we would add those two values together (because they are the "squared differences averaged") to get a final 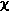 2 = _.
2 = _.
In other words, when the chi-square equals zero the experimental results are in exactly the ratio ________!
Conversely, the _______ the chi-square gets from zero the less likely the ratio "rule" is being followed.
We could have got a chi-square value as high as ____ and still feel that we were close enough to the 3 : 1 ratio to not be worried.
Here's another set of results from Mendel's monohybrid cross experiments. Let's do the chi-square analysis of it.
P = green seeds crossed with yellow seeds
F1 = all yellow seeds
(So which color is dominant?)
[______]
F2 = 6,022 yellow seeds and 2,001 green seeds
First, calculate the ________ number of each type.
You have a total of 8,023 seeds (6,022 yellow + _____ green = 8,023).
The green seeds should make up a quarter of that population, so dividing 8,203 by _ gives you 2,005.75.
That means you ________ 2,005 and ¾ seeds.
The yellow seeds should make up the rest of the sample so we can find their number by subtracting 2,005.75 from the total 8,023 to get ________.
So, from the total of 8,023 seeds you expected 6,017.25 to be yellow and 2,005.75 to be green.
Second, calculate the "_______ ___________ per ________".
You expected 2,005.75 greens but ________ 2001 and that is a difference of 4.75 (2,005.75 - 2,001 = 4.75).
Square that number you get _____. Divide it by the number you expected (________) you get 0.011.
You expected 6,017.25 yellows but observed 6,022 and that is a difference of 4.75 (6,017.25 - 6,022 = -4.75). Square that number you get 22.56. Divide it by the number you expected you get (6,017.25) to get _____.
Third, add up the "squared differences per expected" from ___ the categories. That's 0.011 + 0.004 = 0.015 so your 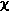 2 = _____. 2 = _____.
We are working with only ___ degree of freedom.
The ratio observed in this experiment
|
|
The chi-square formula is 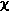 2 =
2 =  [(O - E)2/E]
[(O - E)2/E]
"O" is the number ________ and "E" is the number ________.
The symbol " " (called "sigma") is used throughout math to mean "___".
" (called "sigma") is used throughout math to mean "___".
Let's assume the results of a cross were
3,087 yellow seeds and 2,937 green seeds.
|
There are _____ seeds in total. If the 3 : 1 ratio applies then one quarter of them should be green.
That means 1,506 should be green and the rest (4,518) should be ______. Doing the greens first, that's (O - E)2/E = (2,937 - 1,506)2/____ = 1359.7 The yellows will be (O - E)2/E = (_____ - _____)2/4,518 = 453.2. Now add them together (that's what S means) to get a 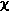 2 = ______. 2 = ______.
|
|
Our calculated chi-square shows that these experimental results are well _______ the acceptable range for a 3 : 1 ratio so we ______ the idea that these results represent a 3 : 1 ratio.
What ratio are they close to and how would you test the ratio to see if it is close enough?
[______________________.]
Do another chi-square on that same data (3,087 yellow seeds and 2,937 green seeds) and see if it is close enough to a _ : _ ratio.
|
There is a total of 6024 seeds so a 1: 1 ratio should show us
3,012 yellow seeds and _____ green seeds. The greens will be (O - E)2/E = (2,937 - 3,012)2/3,012 = _____. The yellows will be (O - E)2/E = (_____ - 3,012)2/3,012 = 1.867 (again). Adding them together gives me the 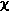 2 = 3.734 and compare that with the Table. 2 = 3.734 and compare that with the Table.
|
|
The new 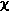 2 , using a 1 : 1 ratio, is low enough to be within the range of significance. (This
2 , using a 1 : 1 ratio, is low enough to be within the range of significance. (This 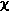 2 is less than 3.84.)
2 is less than 3.84.)
Therefore, the results of this experiment are too far from being 3 : 1. I think they are ______ 1 : 1.
The chi-square is used whenever you want to compare the observed results to the ones you would expect from a certain ____. That ratio could be 1 : 1 or 1 : 3 or even 9 : 3 : 3 : 1.