Principles of Astronomy is copyright protected, is the sole property of the author (Dr Jamie Love © 1997 - 2011) and is sold exclusively by Merlin Science. Any form of reproduction by any media is strictly forbidden.

Getting your Bearings

by Dr Jamie Love © 1997 - 2011

It just so happens at this point in Earth's history that our planet's axis of spin points directly to Polaris, the "North Star". [That's not completely true but it's pretty close. Polaris is less than 1 degree from true north.]
This causes many interesting astronomical effects that you should know and understand. Polaris is always above the North Pole so by finding it you can find which way is north. Also, by measuring its angle from the horizon you can use Polaris to determine your latitude. [Latitude is your angular location with respect to the Earth's Equator.] Of course, that assumes you can see Polaris. You can't see Polaris from the southern hemisphere. And finally, you should appreciate the fact that all the stars appear to circle Polaris at a constant rate and that allows you to keep track of the spinning of the Earth and thus the time.

How do you find Polaris? Is it the brightest star?

No, Polaris is not the brightest star. There are probably a hundred stars brighter than Polaris. Yet, it is still easy to find by using "pointer" stars from URSA MAJOR (The Big Bear) to point to it.

Part of URSA MAJOR forms the easily spotted Big Dipper. By the way, the Big Dipper isn't a true constellation. It's a "pseudo-constellation" (and that is why I only capitalize the first letters). The stars of the Big Dipper are very bright. Four of them form a "bowl" and three others make a handle. Here I've drawn the Big Dipper in a horizontal position so it's easy to see the pattern, but you should be aware that the Dipper may be tilted at any angle, depending on the time and date.

Let's take a good, long look at the stars in the Big Dipper. It isn't important to get the pronunciation right. You might want to memorize the names of these stars - it will get you used to some of the strange names, most of which go all the way back to Ancient Arabia. Also, we will be talking about these seven stars in subsequent lessons.

Starting at the end of the handle and working to the opposite edge of the bowl, the stars of the Big Dipper are: Alkaid, Mizar, Alioth, Megrez, Phad, Merak and Dubhe. The last two, Merak and Dubhe, are the "pointer stars" that take us to the "North Star" (Polaris) so they are well worth knowing.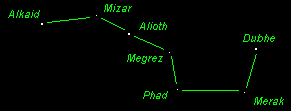

When the sky is better (no clouds, Full Moon or lights interfering) there are more stars and this image gets more complicated, but it also gets more interesting.

Here's the Big Dipper again but this time on a clearer night when you can see more stars. Look at Mizar, the middle star in the handle. On a very clear night you can see its companion star, Alcor. (Binoculars help.) Our line of sight makes them appear to be side by side but, in fact, they are (probably) separated by three light-years. (A light-year is the distance that light travels through the "vacuum" of space in a year. It's about 10 trillion kilometers or 6 trillion miles.)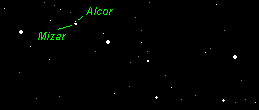

For comparison, the Sun's nearest star, Alpha Centauri, is a little over 4 light-years away. So Mizar and Alcor are no more linked than we are to Alpha Centauri. Pairs of stars like Mizar and Alcor that appear to be together (like this) are called "optical doubles". If you were circling either Mizar or Alcor and used a telescope to observe the Sun, you would see that Alpha Centauri and the Sun form an optical double.

Alcor is a great way to test your vision and the "quality" of the night sky. If you can see Alcor, your eyesight is good, you are far from lights (such as streetlights or moonlight) and the sky is clear. Perfect for astronomy!

So, how do you find the North Star?

Now that you know the Big Dipper, it's easy to find the North Star! Imagine a line from Merak to Dubhe.

Then imagine that line extended through Dubhe about five times as far as the distance between Merak and Dubhe. The bright star you come to is Polaris, the "North Star". It's in the end of the handle of the Little Dipper, another "pseudo-constellation". I haven't drawn the green lines of the Little Dipper because you should learn to imagine them yourself. (After all, my green lines won't be there to guide you in the real sky - just the stars!) The Little Dipper is actually part of the constellation called URSA MINOR (The Little Bear). Unfortunately, the Little Dipper isn't as obvious as the Big Dipper.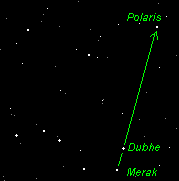

Most of stars of the Little Dipper are pretty dim but the brightest of them is Polaris. However, you should understand that in a poor ("quality") night sky you may not be able to see all the stars of the Little Dipper.

Notice how the handles on the two dippers bend (arch) in opposite directions. The Big Dipper's handle arches in the same direction as the bowl. The Little Dipper's handle arches away from its bowl.
Also notice that they appear to be "pouring" from one to the other. They always look that way - as the sky rotates the two dippers look as if they would be pouring something between them.

Cool. Now, how do you figure out your latitude?

The North Pole is always at a latitude of 90^o and Polaris is always above the North Pole (approximately) so Polaris has a "sky latitude" of (approximately) 90^o. The Equator always has a latitude of (exactly) 0^o. The angle formed between Polaris and the immediate northern horizon can be measured accurately using a device called a sextant. A sextant originally measured angles within a 1/6 slice of a circle (60^o) and that's how it got its name. For hundreds of years sailors, explorers and astronomers used a sextant and Polaris to figure out their latitude. To find your latitude simply measure the angle from the northern horizon to Polaris. There are a variety of different ways to make this measurement. Use your imagination.
[If you don't have an imagination, ask a math or science teacher. ]

Is there a rough way to make the measurements?

Yes, use your hands! Extend your hand towards the sky and spread all your fingers out as wide as you can. If you look along the length of your arm, the "distance" between the tip of your thumb and the tip of your little finger covers (about) 20^o of the sky. You can "walk" one hand over the other as you count how many open handfuls of sky it takes to reach Polaris from the northern horizon. Your fist, with the thumb tucked in, covers only (about) 10^o when used the same way.

So, you can use your hands to measure angles in the sky. Face north and spread out your right hand, placing the tip of your little finger on the northern horizon so your thumb is pointing up. Remember, your hand must be positioned so that you cover the maximum distance with your thumb and little finger. Now place the tip of the little finger of your left hand on the tip of your right thumb and continue "walking" up the sky towards Polaris. When you get close to Polaris use your fist for the final measurement or two, if you must. Add up how many wide open hands (20o) and fists (10o) it takes to go from the northern horizon to Polaris and you have figured out your latitude. (Roughly.)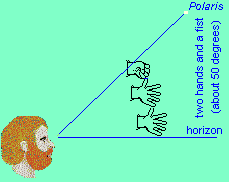

You can try to be more precise by knowing that each of your fingers covers between two and three degrees of sky, when held at arm's length. (Don't get too carried away with this. These measurements are only approximate - "off hand"! )

How do you use the night sky to tell the time?

Because the axis of the Earth points to Polaris, the stars appear to revolve around it at a constant rate. It's possible to tell the time using Polaris and another star (Merak, for example) but you have to know how to correct for the date. That's a bit complex but not impossible.

However, it isn't difficult to imagine how to tell how much time has passed by. In any twenty-four hour period a star will return to its original position.
[Actually that's not totally true. Each star will be slightly ahead of yesterday's position because of the Earth's movement around the Sun, but between any two days that difference is small. You would have to take careful measurements to notice that daily change.]
Therefore, Merak (like all stars) will revolve all the way around Polaris and return to its original place in 24 hours. That means in 12 hours it will be 180^o from its original position in the sky, on the "other side" of Polaris. Or in 6 hours it will be 90^o from its original position. In just 1 hour any star will be 15^o from its original position in the sky. In fact, even Polaris will move by this same amount around true north, but it's very difficult to see that difference.

As you stare towards Polaris, imagine a "sky-clock" imposed upon it. This sky-clock has two features that make it different from any clock you've ever seen.
First, it's a 24 hour clock not a 12 hour clock, so it has the numbers one through twenty-four arranged on it, each 15^o apart. [A regular clock has only the numbers one through twelve arranged 30^o from each other.]
The other important thing about the sky-clock is that it runs backward! The stars revolve around Polaris in a "counter clockwise" (or "anti-clockwise") direction.

Polaris is at the center of the sky-clock and any star (Merak in my example) is an hour hand.

So, how do you tell how much time has passed?

Let's say you've decided to stargaze for two hours. In two hours the sky will have revolved 30^o (that's twice 15^o per hour).

The sky now.

Imagine a line drawn from Polaris to Merak. Then imagine another line drawn from Polaris but 30o counterclockwise from the first line. Make a note where that second line meets the horizon. Two hours later Merak will be along that second line. Study these two images and understand that the one of the right shows that the Dipper (and all other parts of the sky) has rotated 30o counterclockwise.

The sky two hours later.

You can use any star you want to be the hands of the clock but you must always use Polaris as the center. Merak is nice because it's bright and you also use it to find Polaris. However, I like to use Phad because it's close to a "right ascension of twelve hours".

What are you talking about?

I'm talking about another important concept in astronomy that will help us with our observations. Polaris is the "center" of our clock - you can't argue with that. However, we could pick any place to start our clock. Astronomers have agreed which part of the sky to call "zero hour" and that sets the standard we all follow.

It is convenient to imagine the night sky as a giant globe in which we (the Earth) are centered. This allows us to use coordinates to describe places in the sky, just like we use longitudes and latitudes to describe points on the Earth.

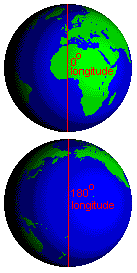
Take a look at a globe of the Earth. It has a zero longitude that runs from the North Pole, through England, through Spain, down through the west side of Africa where is passes the Equator and then continues all the way down to Antarctica and the South Pole. People agreed to define this line as the "zero degree longitude"(0o). Any line that goes from pole to pole along the surface of the Earth is a line of longitude and any such line could have been called "zero degree longitude" but it was agreed to use this one so we would all know which longitude line we were talking about when we said "zero degree longitude"(0o). Look at the line that comes up from the South Pole on the other side. It passes near New Zealand, goes over the Equator, cuts the edge of Siberia and ends up at the North Pole. It's a longitude of 180 degrees (180o) because it is on the opposite side of the Earth - opposite the zero longitude that ran through England (Spain, etc.).

Together, both these lines of longitude create a circle around the globe. Indeed, any two lines of longitude that are 180 degrees apart will form a circle around the globe.

Now imagine a line through the sky that runs from Phad through Polaris and beyond. If you extend that line on both sides it meets the horizon at opposite ends of the sky. If you could continue those lines you would see that they meet on the opposite side of the Earth (right under your feet) creating a giant circle. That is our special "sky longitude". The line from Polaris to Phad is like the 180o longitude line on the globe. The line going from Polaris to Chaph is like the 0o longitude line. Actually, we don't call it a "sky longitude". Astronomers call it a line of right ascension and rather than measure these lines in degrees we use hours. (You'll see why soon.) The line from Polaris to Chaph is on the line defined as zero hour right ascension (0h). Imagine Chaph was due south at some particular time. Twelve hours later it would have moved to the other side of the sky and be due north. Phad would now be due south. Therefore Phad is on the twelfth hour right ascension(12h).

Chaph is not exactly on the line of zero hour right ascension and Phad is not exactly on the twelfth hour right ascension line either! They are merely close to these imaginary lines. (For that matter, Polaris is not exactly at true north, but it's close enough.) By learning to recognize Phad and Chaph you can get a rough idea about the right ascension lines and make estimates of the right ascension of other stars.

Here I've drawn the even numbered right ascension lines. See how they radiate away from Polaris in all directions? I know this image is a bit thick with confusing lines, but try to imagine it on a real night sky and imagine how the stars would move as the hours pass by. Notice that the clock rotates "backward" but the numbering of the right ascension lines is clockwise. [If you think about the Earth's direction of rotation you'll understand why. More on that later.] Pick out Chaph near the zero ascension line (0h) and Phad near the twelfth hour ascension line (12h). Merak and Dubhe follow the eleventh hour ascension line (11h) very closely. That means after 11 hours have passed, Merak and Dubhe will be in the same direction that Chaph is in now. Look at Alkaid at the end of the Big Dipper's handle. Alkaid is near 14 hours of right ascension so in 3 hours it will have moved to (roughly) the position of Merak and Dubhe.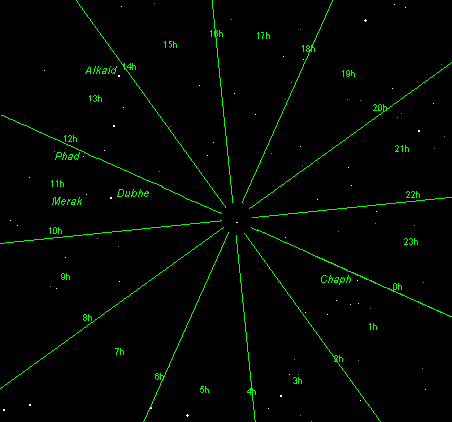

What is Chaph?

Chaph is a star in the constellation called CASSIOPEIA. Cassiopeia was an ancient queen and this constellation represents her sitting on her throne. (You really have to use your imagination! ) You should learn to recognize this constellation. It's pretty easy to find.

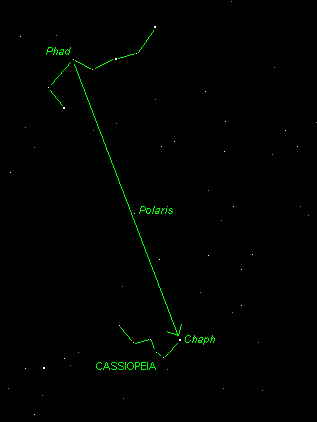
CASSIOPEIA it is always opposite the Big Dipper - just draw a line from Phad through Polaris and continue it on about the same distance and you will come to CASSIOPEIA. This is the same line you follow to define the 12 and 0 hour right ascension lines. CASSIOPEIA is bright and has a distinctive W-shape. Note that the "W" might be at any angle due to the Earth's rotation so sometimes it will look like an "M". Chaph is at one end of the "W", but which end? If you look carefully at CASSIOPEIA you will notice that it's a lopsided "W" as if the left side has been bent down too far. Chaph is at the other end of the "W" that hasn't been damaged. You'll also notice that Chaph is the brightest of the stars in the "W". You should now be able to identify one constellation (CASSIOPEIA) and two "pseudo-constellations" (the Dippers) in the northern night sky. In this image you can't see all the stars of the Little Dipper because they are so dim, but you should use your imagination (and memory) to "fill in" the missing stars. That's good practice for any astronomer because clouds and moonlight can hide dim stars.

When will the stars near Polaris set?

Stars near Polaris never really set. Instead they circle the pole without dipping below the horizon. Stars with this behavior are called circumpolar because they circle the pole. However, ALL stars circle the pole, so when we describe a star as circumpolar we mean it is ALWAYS visible circling the pole star. (On a clear night, of course.)

Which stars are circumpolar depends upon your latitude. At a latitude of 90^o (the North Pole) all the stars you can see are circumpolar. At a latitude of 0^o (the Equator) none of the stars are circumpolar. To determine which stars will be circumpolar from your location, think about your latitude. If your latitude is 37^oN then all stars within 37^o of Polaris will be circumpolar and thus always visible in a clear night sky. Any stars further than 37^o from Polaris will rise and set - they will not be circumpolar.

There's a lot of info here. Do I get homework in this course?

Of course! (But I won't check it. )

Find some time this month on a clear evening to look at the two Dippers and find Polaris. If possible, try to make your observations a few hours apart in order to appreciate how the sky rotates around Polaris. Imagine the lines of right ascension - zero for Chaph, 11 for Merak and Dubhe (the "pointer stars"), 12 for Phad, and 14 for Alkaid.
Practise using your hands to measure angles in the sky. Measuring angles is a very important technique for an amateur astronomer. So is the ability to find Polaris, Phad and Chaph.
Determine which stars will be circumpolar from your latitude. What is the maximum angle they can be from Polaris? Use your hands to measure that angle from Polaris to the horizon in any direction. Repeat that measurement choosing different horizons in order to determine which stars are circumpolar. Is Phad circumpolar? Is Dubhe circumpolar? Is Chaph circumpolar?
While you're at it, imagine how the position of Polaris would change if you were to walk to the North Pole. As you reached the North Pole, where would Polaris be? Directly over head (at your zenith)? On the horizon? Now imagine you walked to the South Pole. At what latitude would Polaris disappear as you walked south? Imagine how the circumpolar stars would change as you walked from the North Pole to the Equator.

If the sky is constantly spinning, how do I keep track of my observations?

That's a good question and it's the topic of our next lesson - The Earth's Motion.

Principles of Astronomy is copyright protected, is the sole property of the author (Dr Jamie Love © 1997 - 2011) and is sold exclusively by Merlin Science. Any form of reproduction by any media is strictly forbidden.