This work was created by Dr Jamie Love and licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.

PRINCIPLES OF ALCHEMY AIR The "air" of the universe, hydrogen and helium. Isotopes are the variations of the elements. Transmutation changes the elements. Dalton: creator of Modern Atomic Theory. The symbols & hieroglyphics of Modern Chemistry. Nuclear Radiation: The types of atomic energy and how we count it. Creation of all the atoms in the Universe. Bohr's shells are the first step to understanding electrons. Atoms are shaped by their orbitals. It's just quantum mechanics!

The universe is full of hydrogen. In most places it is rather sparsely distributed, as in the vacuum of space. But in some places hydrogen is so thick that it creates stars. Hydrogen is the first of the elements. It's the oldest, the smallest, the simplest and the most abundant of the elements. It makes up over 74% of the Universe! Another element, helium, makes up another 24%. So together, hydrogen and helium, the "air" of the universe, make up 98% of everything there is. Understand them and you will understand 98% of the chemistry of the universe! That is the goal in our first lesson.

Hydrogen is an atom and atoms are very, very small. Invisible. Atoms are the smallest units of matter that keep their chemical identity. The name "atom" is from the Greek for "indivisible", because you cannot break up an atom any further and still have a chemical.

Sub-atomic particles, not a chemical. It wasn't until late in the 19th century that people started thinking that there might be something smaller than an atom. We still use the Greek word "atom" even though it is made of smaller particles.

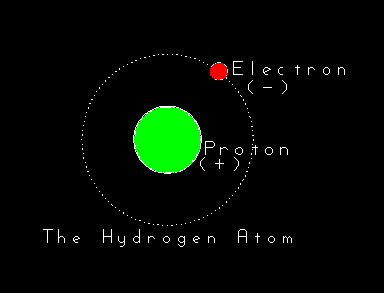
It's convenient to imagine atoms as tiny spheres around which orbit smaller spheres (dots!) of opposite electrical charge. This is a sufficient and workable image on which to build an understanding of Modern Alchemy (chemistry). Be warned, however, that this picture of atoms breaks down at the level of detail and understanding required by physics. But for the purposes of Alchemy it is good to think of hydrogen as a single, positively charged sphere called a proton. Protons are in all atoms. Hydrogen IS a proton. And that is why hydrogen, the first element, is also the simplest, smallest and most abundant element. Hydrogen is the fundamental element upon which the Universe is built!

That’s it?! Hydrogen is just a positive bit of tiny, invisible matter?

Aye. But at the temperatures and conditions at which most chemistry takes place, these protons (hydrogen) have a companion particle called an electron. Electrons carry a single negative charge, equal but opposite to the proton's charge. And electrons are much smaller than protons. It would take over a thousand electrons to give you the same mass as one proton. The hydrogen's electron orbits the proton, being attracted to it by the opposite charge, but restricted from actually reaching it (by laws best dealt with in an advanced physics class). Notice that the positive charge of the proton is balanced by the negative charge of the electron, so the entire hydrogen atom has a "net" charge of zero.
Like this: +1 (proton) and -1 (electron) gives a total charge of 0. That's a complete, neutral hydrogen atom.

Not quite. Most of the hydrogen in the universe is ionized. That is, the number of electrons is NOT equal to the number of protons. An atom which has an UNEQUAL number of protons and electrons is called an ion. Ions always have a "net" charge. Either positive, if it has more protons than electrons, or...

That's right. Stars are mostly hydrogen ions because they are so hot that the electron flies off! These hydrogen ions have a charge of +1.

Right.
Time for a review. Everything in the universe is made of atoms. The simplest, smallest and most common atoms are hydrogen. It has a single positive proton and often a single negative electron circling it. That gives the hydrogen atom a net charge of zero. If the hydrogen is very, very hot, like in a star, it looses its electron. It will have a net charge of positive one (+1) from that one proton and we say it is ionized.
Because hydrogen is so simple, I like to say that hydrogen is the first element.

Didn’t I? Oh dear. Well, elements are substances made entirely of atoms with the same number of protons. Chemicals are made of elements and elements are made of atoms. Gold is an element. If you break up a piece of gold, it gets smaller and smaller until all that is left is a single gold atom. If you cannot break it down any further, you know you have an element.

Aye, it is! A coin of pure gold is a pure element. You can break it into smaller gold pieces, but you cannot break it into anything else.
Hydrogen is the most common element and gold one of the rarest.

That would be a compound. Compounds are made of two or more elements. Water is a compound because, if you work at it, you can break it up into two different types of atoms or elements. In your next lesson I will teach you about water. Today I want to keep things simple and just talk about elements and the atoms that define them.

Yes, precisely! There are about a hundred different elements, gold and hydrogen just being two of them.

Yes, that’s right. Oh, but you would also get some neutrons out of most atoms or elements which you broke up.

Yes. They are the other things inside atoms. Neutrons are at the center of the atom, along with the protons, and they are about the same size as a proton. But neutrons do not have a charge.

Aye. That’s why we call it a neutron. It’s neutral. I like to think of neutrons as the ghosts of atomic particles. They hide in the center of the atom along with the protons, but you can’t detect them by their charge. They contribute nothing to the atom’s chemistry. They’re just extra mass. That brings us to an important point.
Protons define the element. Hydrogen is hydrogen because it has one proton. Gold is gold because it has 79 protons.

Yes! And it's the number of protons which give an atom its chemical properties.
Hydrogen behaves the way it does because it has only one proton. Gold behaves the way it does because it has 79 protons.
The chemical behavior of each and every element is determined by the number of protons, and the number of protons defines what the atom or element is called. The number of protons in an atom is the atom's atomic number.

Yes, that's right. But you'll never find an atom with that many protons. The biggest naturally occurring atom has an atomic number of 92.

Yes, it is. Alchemy isn't difficult.

Enough of that!
You can see that the atomic number is the first thing you would want to know about an atom, because it tells you how many protons it has and thus what element it is and how it behaves.

Oh. Neutrons do nothing to define the element and they have nothing to do with the atom’s chemistry. They add extra "weight". But I like to think of them as adding extra mass. Weight is just an "earthly" term. We Alchemists speak of the mass not the weight of atoms. More on that later.

Ah, well, sort of right.
Most hydrogen is just a proton, but some hydrogens have a neutron too. As a matter of fact, some even have two neutrons. But they are still hydrogen...

Right!

We say they are isotopes of hydrogen. Isotopes of an element have the same number of protons (that’s why they are a single element) and have the same chemistry (because they have the same number of protons). But isotopes have different masses because they have different numbers of neutrons.

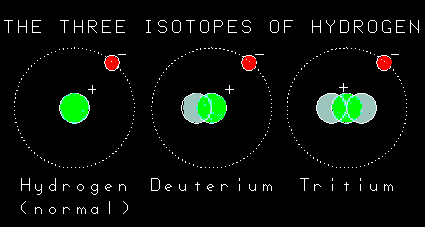
But they're all called hydrogen. Ah, sort of. Because hydrogen is the most common element, people decided to give names to the hydrogen isotopes. It is fair to call all hydrogen isotopes hydrogen, but we can be more specific. If the hydrogen has one neutron, it is called deuterium and if it has two neutrons we call it tritium. And if it doesn’t have any neutrons, just a proton, it is called hydrogen?

Yes. It seems strange, but the element called hydrogen (which always has just one proton) can have no neutrons, one neutron, or two neutrons. The hydrogen with no neutrons, doesn’t have a special name, but the two other hydrogen isotopes have names of their own. Strange isn’t it?

It gets easier. But you must understand that all elements are defined by the number of protons. The various isotopes of each element differ only in the number of neutrons.

That would be helium and I’m glad you brought that up. Helium is the second smallest, second oldest and second most abundant element (or atom) in the universe. Helium is identified by having two protons.

You bet right. Fortunately, the different helium isotopes do not have their own names. Helium can have either one or two neutrons. But helium can never have no neutrons.

Good question. Helium atoms without a neutron are too unstable to last. They disappear faster than you can blink!

Because there are certain combinations of protons and neutrons which work and some that don’t. It all has to do with the way they interact in the center of the atom, the nucleus (plural nuclei). The exact reason is understood by only a handful of physicists and is not important to understanding Alchemy. But a good Alchemist is aware that some isotopes are stable and some are not. Some, like helium without a neutron, disappear instantly, while others like tritium take years to disintegrate.

I don’t know. I suspect it has something to do with the "magical" world of sub-atomic physics. I am not trying to teach you that anyway. Let’s stick to Alchemy, shall we?

OK. Are all the hydrogen isotopes stable?

No. Tritium disintegrates. But slowly. It takes about 12 years for half of it to disintegrate. And another 12 years for half of that to disintegrate. And so on.

First, let me tell you about this kind of disintegration and then you can tell me what tritium becomes when it disintegrates. This is called beta decay and here is how it works.
Tritium has a proton and two neutrons, right?

One of tritium’s neutrons turns into a proton. It's like magic!
Now tell me, if that tritium atom turns one of its neutrons into a proton, what element has it become?

Right. Tritium disintegrates (or decays, if you like) into helium.

Aye. And it is amazing! In medieval times such as these, wizards and kings would give anything to change one element into another. Even the best Alchemists can’t do that. But nature does it all the time. And always at a constant rate.

Transmutation (and it is NOT magic). When one element becomes another it is transmuted. This is an unusual angle on chemistry, and is really a topic for physics. But any good Alchemist should be aware that it occurs.
Now here’s a thought. The mass of the old tritium and the new helium are the same, because protons and neutrons have the same mass. There’s a total of three particles in each.
Nothing has really changed except the charge.

And it always applies.

That would be right if that were the end of the story, but it's not. The total charge, or "net" charge, remains unchanged because as the tritium turns a neutron into a proton, it also makes an electron and spits it out!

OK! OK! I was trying to keep this simple you know. I’m trying to teach Alchemy here not physics!

Well, the truth is, the mass of the neutron is very slightly heavier than that of a proton.
And before you start to give me more trouble, let me repeat, I’ve been trying to keep this simple!
So when the neutron turns into a proton, the electron is created from the difference in mass. And the opposite charge of the new electron balances out the positive charge of the new proton. All is in balance. Nothing is created from nothing! All I want you to understand is that the (very slightly heavier) neutron disintegrates into a proton and electron. Which together means that no new charges or mass are created, just rearranged. Do you understand?

I think so. One of the neutrons in tritium turns into a proton and an electron. Because an extra proton is created, the nucleus now has two protons and so it is no longer the element hydrogen. It has been transmuted into the next element, helium. And an electron is spit out too, so there is a balance of charge. Because you can’t get something from nothing! Even the mass is the same because the mass of the new proton plus the mass of the new electron equals the mass of the old neutron. Right?

By Jove, I think you’ve got it! Now, I want you to think about that electron again. I said it was spit out of the nucleus. Remember?

It goes flying far away. It escapes from the newly formed helium like a rocket! That electron moves away at such a tremendous speed that it can cause damage if it hits you. You do not want to get hit by too many of these flying electrons!

No. You’ve got it backwards. It's the tritium that is dangerous because it spits out a fast moving electron as it decays into helium. The tritium is unstable, but the helium it becomes is stable. When an isotope transmutes (changes from one element to another), it spits out particles and rays, and we say it is radioactive. It is that "radioactivity" which is dangerous. Got it?

Good. So tell me what you have learned about beta decay of tritium and its transmutation into helium.

That’s right. Now let’s put some names and numbers to how we describe these things. The protons and neutrons, the two things in the atom's nucleus, are called nucleons. Nucleons make up most of the mass of an atom, the rest of the mass is just the very light electrons. When we talk about the mass of an atom, we are only referring to the total number of nucleons. We don't count the electron's mass. Normal hydrogen with its one proton has a mass of one. It has only one nucleon. Deuterium, has two nucleons (one proton and one neutron) for a total mass of two. How many nucleons does tritium have?

Right! So the element Hydrogen has three isotopes - with one, two or three nucleons. But they are all the same element because each of those three isotopes have only one proton.

If we were to weigh them we would find that the tritium weighs three times as much as the normal hydrogen. And a normal hydrogen would weigh only half that of a deuterium atom. Do you understand why?

Right!
We think of the hydrogen atom (actually its proton, because that's all there is to normal hydrogen) as the fundamental unit of chemistry.
And this is a good point to mention units. You know, how we count in chemistry.
Rather than talk of something's weight, we think in terms of its mass. Mass is a much better way of describing something. The weight of something can easily change without the atoms changing. All you have to do is take it away from the Earth or move it around rapidly. But its mass doesn't change. Its chemistry is still the same. The mass is constant! The mass of a hydrogen (proton) is exactly One Dalton.

Says Dalton! He was a genius. Lived just a few miles from here. John Dalton was one of England's great natural philosophers. In 1808 he wrote a book called New System of Chemical Philosophy. It changed the way we think about matter and was a critical step in the evolution of Ancient Alchemy into Modern Alchemy (chemistry).

Well, it was! But it was not like most philosophy books. Dalton argued that for each chemical element there is a different kind of atom. He explained that different materials are different combinations of these atoms. Dalton was so important that Alchemist use his name for the fundamental mass of atoms.

Correct. Protons and neutrons each have a mass of a Dalton. Or close enough. (Don't start on me about the tiny difference in weight between the proton and neutron!) Put another way, the mass of a nucleon, either proton or neutron, is one Dalton. What is the mass of the other isotopes of hydrogen?

Not "WEIGHS"! It has "a MASS OF" two Daltons. It might weigh ten pounds in one part of the universe and nearly nothing somewhere else. But deuterium always has a MASS of two Daltons.

Now you've got it!
What have you learned so far?

Good!
The atom's atomic mass is the number of nucleons it has.
Don't get it confused with an atom's atomic number, which is the number of protons it has.
Tell me, what are the atomic number and atomic mass of helium?

Correct. And helium's atomic mass?

Is it? Is it always? Do all helium's have an atomic mass of four? Do all helium atoms have four nucleons?

That's right! You see, helium ALWAYS has an atomic NUMBER of 2....

Right. But helium doesn't always have two neutrons.

Yes.
Sorry if you feel I have mislead you. I want you to see what you can and cannot figure out directly from knowing what element it is. Atomic NUMBER tells you the ELEMENT, but atomic MASS tells you the ISOTOPE.

That's right. But the atomic mass of an element...

Almost anything. The atomic mass can never be smaller than the atomic number. Do you know why?

Absolutely!

That's right. But it wasn't a trick. It was an example of what you can figure out if you know what you are doing.

That's right. Sort of.
In the 20th century they have ways to measure the atomic mass of atoms. But we will often refer to an atom's mass, its atomic mass, as if we had measured it. The mass of all the elements, actually their various isotopes, can be found in any good chemistry book.

Yes, it would and yes, there is. It's called relative atomic mass and here's how it's calculated. We measure all the helium isotopes and figure out how much of each is present in the universe and in what proportions.

No, not really. We estimate the relative proportion of the element's isotopes and come up with a number which represents its relative atomic mass.

With sophisticated machines in the 20th century. It works like this. An extremely pure sample of the element is weighed and its mass calculated. Because the sample contains a representation of all its isotopes, each of a different mass and occurring in different proportions, it acts as an "average" for all the isotopes.

An example might make it clear.
As it turns out, the most common isotope of helium has four nucleons, or an atomic mass of four.

Well, all the other helium isotopes are much, much rarer. But they do make a contribution to the total population of helium. So it would be wrong to ignore them. Let's say, just for this example, that for every 1000 helium atoms with an atomic mass of four Daltons, there is one helium atom with an atomic mass of three Daltons. If you were to measure the mass of all 1001 of those helium atoms, and then divide by 1001, you would get the average atomic mass for that collection of helium atoms. Right?

Yes, indeed!
Tell me. What would be the total mass of 1000 helium atoms with four nucleons plus that one lighter helium with only three nucleons?

Yes. Now what would be the average mass for those atoms?

You can do it if you like. But tell me, will it be four?

That's right! 3.999000999 to be exact. (Don't ask me how I do those big numbers. It helps to have a 20th century calculator!)

Yes, it would be. But only if there were 1000 heliums with four nucleons for every one helium with only three nucleons. However, the universe is more complex. I've used the 1000 to 1 ratio to make the math easy.

It could be worse. The ratio of those two isotopes of helium is a lot larger than 1000 to 1. And we haven't considered the other helium isotopes. You know, the ones with five or six nucleons (three or four neutrons).

It is. But not difficult to understand. 20th century Alchemists have sampled parts of the earth and some parts of space and they have worked out the ratios of all these elements. They have calculated the relative masses of each element from that data.

4.0026

Yes, it is. What does that tell you about the isotopes of helium?

Absolutely right.
Each element has a "most common isotope". Helium's most common isotope has four nucleons and it has an atomic mass of 4 Daltons. But when you average in all the other isotopes of helium, each in the proportions found in the universe, you get the relative atomic mass of 4.0026.

Sometimes. But not usually.

Because in some forms of Alchemy it IS important. And when you look up the relative atomic mass of an element (in one of my 20th century books) you will understand how it can have numbers which are not whole numbers.
Believe me Arthur. By learning these basics with simple atoms, like hydrogen and helium, you will have the ability to do it for the more complex atoms. You'll see.

Good.

We've been using a rather awkward way to describe these atoms. I think it's time I taught you how to talk and write like a proper Alchemist!

Not quite.
Like saying "helium four" instead of saying "helium with four nucleons". It is easier to say. Don't you think so?

By Jove, yes it is! What's another name for deuterium?

Right. Easy isn't it?

Exactly.
Now let's talk about how we go about writing down these isotopes and elements.
First, we abbreviate the elements. Hydrogen is simply "H".
Second, we list the number of nucleons in the element just above and to the left of the letter. Like this: ¹H. That's simply hydrogen with one nucleon. And that nucleon has to be a proton, or it wouldn’t be hydrogen. Right?

Now deuterium has a proton and a neutron. So it has two nucleons and we abbreviate deuterium as ²H. By the way, we pronounce this "hydrogen-two", even though it is written with the number first. If we called it "two hydrogen", people might think we were talking about two hydrogen atoms, not a type of hydrogen.

Yes.
Tell me, Arthur. How would you abbreviate tritium?

Right. This simple way of abbreviating the atoms allows us to describe them better. The letter reminds us which element we are talking about and the number of nucleons tells us which isotope.
Recall, it is the number of protons which determines the way the element behaves. But it is the total nucleon count which tells us it’s mass. Hydrogen’s three isotopes are ¹H, ²H and ³H.

Yes.
About 74% of the mass of the universe is hydrogen. And 99.985% of that hydrogen is the simplest type, the ¹H. Only 0.015% of the hydrogen is ²H (deuterium).

Good question. Tritium is very, very rare! So rare that it doesn’t show up in the count. It would take a lot of zeros to show it as a proper number. We’ll talk about that some other time. For now, let’s just say there is only a tiny trace of tritium around.

You read my mind. That was to be my next topic.
Helium makes up about 24% of the universe. So together hydrogen and helium account for 98% of the mass of the entire universe. Those two elements make up so much of the universe, I like to think of them as the air of the universe.

That’s right. There are about a hundred different elements, so we have to use two letters for some to avoid duplication. The abbreviation for helium is "He". And it has four possible isotopes. Can you tell me how they would be abbreviated?

Think about it. Think about the structure of helium’s nucleus and the nucleons it is made of.

That’s a good guess, but not correct.

Sorry Arthur. Your thinking is correct, but an atom containing two protons with no neutrons is so unstable that it disappears in the blink of an eye. Remember, I talked about that earlier

Not quite. Tritium takes years to decay. Tritium is unstable, but at least it lasts long enough to find it (if we want to). But ²He is so unstable it disappears before anyone can see it. In fact, I’m not even sure it exists at all!

Absolutely right. And it just so happens that ³He is what tritium (³H) becomes. Remember?

I bet you can even draw a picture showing how tritium decays into helium. Go ahead and try. Just use an arrow to show which way it goes as it disintegrates.

Yes. Very good. Now add the electron that is created. Abbreviate the electron as e (for electron) and just to remind you that the electron has a negative charge, put a tiny minus sign on it.

Excellent. Now to really complete it, why not put all the charges in the right place.
Remember, a hydrogen nucleus has a single proton so it would have one positive charge and helium has two protons so it would have two positive charges. Just place them to the upper right of each element.

Perfect! What you have written is called an equation. An Alchemist's equation is a way to write down a change or a reaction. In this case we have an equation for a transmutation.
Specifically, this equation is the equation for beta decay.
By the way, the equation you have written is for very hot elements - too hot to have their normal electrons circling them. At normal temperatures hydrogen would have one electron circling it and helium would have two electrons. Can you write that equation to include the electrons that normally circle them.

Very good. Now why not tidy things up by adding up those electrons on the right? It will look nicer.

That's exactly right. And very professional too. What you have written is a complete equation. Notice that you can add those electrons together, just like anything else. 2e^- is the same as e^- + e^-. One electron was there to begin with (it was with the hydrogen you started with) and the other one was made by the beta decay.
(Of course, in beta decay the newly created electron is thrown out, away from the atom, but here I am just talking about the numbers of electrons involved.)

Yes indeed!

Yes! And that is a fundamental part of understanding chemistry. We Alchemists write balanced equations all the time. Sometimes like these, but often with other elements and their electrons. All we do when we write a balanced equation is show how it started and how it ends up.

Good. We will be using equations a lot as you learn Alchemy. The equation you have just written is for beta decay and it is a particularly difficult one because it is an equation for a NUCLEAR reaction.
By the way, many people mispronounce the word "nuclear". They say it like "newk-lee-ear" or "new-klee-ear".

A lot of people are wrong. "Nuclear" has only two syllables. It's pronounced "new-klear".
A proper Alchemist speaks properly!

Well, it just takes a little practice. Especially if you've been mispronouncing it for years! I think it has to do with the way we say "nucleus" (pronounced "new-klee-us") and "nucleon" (pronounced "new-klee-on").

You've got it!! (Phew!)
In the future we will be writing equations for CHEMICAL reactions. Only in nuclear reactions do you have transmutations of elements and "creation" of new atomic particles. Equations for chemical reactions are easier because the elements don't change and it is easier to understand.

You're welcome!
The reason I directed you to write the equation for beta decay, a nuclear reaction, is because it is a good learning experience. If you can write an equation like that, with all its complex transmutations and "creation" of new particles, then you will have no trouble writing chemical equations.
But today I want to finish our discussion on isotopes.
Now then, ³He is helium’s first isotope, but I said helium had four isotopes. Can you describe the rest.

Absolutely right. And the other two helium isotopes?

Right again. You have just described all four of helium’s isotopes. And, just in case you are wondering, there are no helium isotopes with more than four neutrons. They just aren’t stable long enough to be found. ⁷He does not exist nor does any other helium of higher nucleon count. I don’t know why not. Just a limit on how many neutrons you can cram into a helium nucleus, I guess.

Oh yes indeed! But for this lesson I want us to focus just on the two elements of hydrogen and helium and their isotopes. Any questions?

That would be ⁴He. It makes up nearly 100% of all helium. There is a very tiny amount of ³He and that comes from the disintegration of tritium (³H) during beta decay. The other isotopes of helium are so very rare that you would have to search a huge amount of space to find them. And you’d have to look very fast too because both ⁵He and ⁶He are radioactive. They decay in less than a second.

No. Not at all. You have proven to me that you understand how to describe isotopes. And you will use that knowledge throughout the entire world of Alchemy. If you learn how to describe the isotopes of hydrogen and helium, you should be able to describe the isotopes of all the other elements.
Now, where was I? Hmmmm.
Let me review for you the abundance of the universe’s most common elements and isotopes.
Hydrogen makes up 74% of the universe and 99.985% of that is simply ¹H (just a proton) with deuterium (²H) making up most of the rest and (radioactive) tritium as just a tiny trace.

Right. But ⁴He is the isotope of helium you are most likely to find.

Yes exactly. Now you know 98% of the stuff the universe is made of. Any more questions?

Yeah, about radiation. Who discovered it? And how? Radiation is invisible, right?

Yes, radiation is invisible and that certainly made it hard to discover. But not impossible. In 1896 a French scientist named Henri Becquerel (pronounced "beck-er-L") was working with a mineral called pitchblende. He didn't know it at the time, but pitchblende is radioactive. One day Becquerel accidentally placed a key between one of his pitchblende samples and a piece of photographic film.

Ah, yes. Photographs and film. Hmmm...
In the 19th century folks discovered that light, just a ray of light, could cause chemical reactions in a silver solution. It's a very interesting reaction, really, but I don't want to get into it now. Suffice it to say that photographic films are coated with chemicals which can detect light. Like a chemical version of an eye. OK?

Anyway, Becquerel later used that plate, and when he developed it he discovered an image of the key on it!

Real weird. Becquerel had no explanation for that image. Finally he decided that some invisible particles or light rays from the pitchblende penetrated the photographic container and caused the plate to be exposed. But the key had blocked some of the "light" so a shadow of the key was made.

Aye. But Becquerel was smart enough to figure out what was going on. His discovery lead the way to many important inventions. And his discovery increased our knowledge of many things - from the universe to atoms.

No, there are two other forms of radiation and many different types of radioactive substances beside tritium.

Beta radiation is just one kind of radiation. The other two are called alpha and gamma radiation. We won’t encounter them until we start to study other, heavier elements. Besides, they are more in the area of physics than chemistry.

That’s where the names come from. Of course the Greeks had no idea about radiation. Radiation wasn’t discovered until the 20th century. And as it was discovered, the three types were named after those three Greek letters. They were named based upon their ability to pass through matter.

Sort of. (But remember, there’s no such thing as a ghost!)
Alpha particles are very weak and cannot pass through a piece of paper. Even your skin can block them.
Beta particles are a bit stronger. They can pass through skin and some can even go through a book!

Actually we have discussed them already.
Alpha particles are actually fast moving ⁴He, with no electrons. So alpha particles have a positive charge from the two protons.

Yes. Exactly. And beta particles are fast moving electrons. So they have a negative charge of -1.

Right. And that is why we call it beta decay. In beta decay a high speed electron is spit out of the nucleus. In alpha decay a high speed helium nucleus is spit out. Many different elements have isotopes which produce alpha and beta radiation - spitting out alpha particles (⁴He^-2) or beta particles (e^-).

Gamma rays are extremely powerful and it takes very thick bricks to stop them. Gamma isn’t a particle at all. It is a high energy ray of light.

Yes. Now it is your turn to tell me the three types of radiation.

Very good!

They do it all the time. Nothing can stop radioactive decay. Not even freezing it. The rate of decay is not affected by the chemical or physical state of the sample.

Oh. Well that depends on the particular radioisotope. And that brings us to the subject of half-life.

No, YOU can't have a half life. And neither can I, but a radioisotope can have a half-life (notice the hyphen). The rate at which a radioactive sample decays, its half-life, depends on the specific radioisotope.
Take tritium (³H) as an example. It has a half-life of about 12 years.

And that means, half of a sample of tritium will have decayed after 12 years. So if you start with 1,000 atoms of tritium, in twelve years you would have only 500 atoms of tritium left. And you would have 500 atoms of something else. Can you tell me what those 500 atoms of something else would be?

You "suppose" very well. After 12 years, half of the tritium would have been transmuted to helium-3.

Well, they are tritium and they will do what tritium always does, beta-decay into helium-3. So in 12 more years half of those 500 tritium atoms will have decayed into more helium-3.

Yes, exactly. After a total of 24 years those 1,000 tritium atoms would have decayed into 750 helium-3 atoms, with only 250 of the original tritium atoms left. That's because 24 years is TWO half-lives for tritium. After each half-life, only half the original radioisotope remains. And that's why we call it "half-life". It's the time it takes half of the radioisotope to decay.
Now tell me how much tritium there would be in each successive 12 year interval. Start with 1,024 tritium atoms.

Another good supposition. But the funny thing about radioactive decay is that it is all a matter of probability. With 1,024 tritium atoms, you can be confident that about 512 will have decayed after 12 years. Just like you would be confident that if you flipped a coin 1,024 times it would come up heads about 512 times. But if you only had one coin flip, it might come up heads or tails. One or the other, but you don't know which. That's the problem with probabilities. They can trick you up sometimes. Especially when you are thinking about just one event. Like one coin flip or one tritium decay.

Well, frankly, some folks understand the problems with probability immediately and others don't. But the important thing to understand is that you don't really work with one or even 1,000 atoms at any one time. You work with billions! So it doesn't really matter about the small numbers problem and the probabilities.

No! I'm teaching you both the theory and the practice of Alchemy. A good Alchemist knows both.

Yes and they each have their own half-life. That is, each radioisotope decays at its own rate.

That's right. You have been paying attention, haven't you? Let's consider another radioisotope.
Carbon-14 (¹⁴C) has a half-life of almost 6000 years (5770 years to be exact). Tell me, if I waited 12,000 years, how much of the original carbon-14 would remain?

Yes. I'm glad you caught your error there. In fact we can write down a series of ever smaller fractions to represent the half-life decays. All radioisotopes decay by half during each half-life. So after each half life we have half of what we started with.
Use 1 to represent the "fraction" of radioisotope we start with (actually the 1 means ALL the atoms are the radioisotope). Then we get a series of fractions like this: 1, 1/2, 1/4, 1/8, 1/16, 1/32,........

Yes, or very close to forever. By doubling the number under the fraction line (the denominator) we are halving the entire number. See?

OK. Potassium-40 has a half-life of 1.3 billion years.

No. That's a fact. Some radioisotopes are very patient. Others are not and they have half-lives measured in fractions of a second. It all depends on which radioisotope you are dealing with. So, if I had a rock with only 1/8 as much potassium-40 as it had when it was made (from molten lava), how old is that rock?

Oh, you can do this Arthur. All I'm doing is turning the problem around. If the rock has only 1/8 as much potassium-40 as it started with, how many half-lives have gone by.

Yes. So, how old is it then?

That's right! The rock is 3.9 billions years old. Get it?

That depends on the rock. Some are very radioactive and some are not very radioactive at all. We measure radioactivity using a 20th century device called a Geiger counter (pronounced "Guy-ger" counter).

Aye! A Geiger counter counts the number of particles given off by a radioactive substance. The exact way it does that is best left for a physics class. However, we all express the amount of radioactivity in a substance by the number of disintegrations it has each second.

No (but that's a good guess).
Becquerel's discovery with pitchblende got the attention of a French husband and wife team, called the Curies. They built on his work and found two new radioactive elements, polonium (Po) and radium (Ra). We named the unit of radiation after them. I'll spare you the details. But they studied huge amounts of radioactive decay. One gram of the radioisotope they studied, radium-226 (²²⁶Ra), produces 37 billion disintegrations per second. We now call that much radioactivity a Curie (abbreviated "Ci").
One Curie (Ci) equals 37 billion disintegrations per second (abbreviated "37 bdps").

Yes it is!. We express it as Curies per gram (of rock, or gas, etc.) And that brings us to our last radioactive word. Specific activity is the number of Curies per gram.

Yes. Very good. And if you had a one gram rock which gave 18 and a half (18.5) billion disintegrations per second...

Correct. Now suppose you had a 100 gram rock which gave off 370 billion disintegrations per second (370 bdps). What would be its specific activity?

But we express specific activity in "Curies per gram", not "Curies per 100 grams".

Yes, but 1/10 of what? What are the units of specific activity?

Yes. You're absolutely right! You sound like a real scientist when you say it that way.
It's always a good idea to think of the units you are dealing with whenever you are working on a scientific math problem. It makes what you are talking about clearer.

We all do! The trick is to work your math slowly and orderly. Each person goes about their math work in a different way. But as long as it is clear to them (and correct) then that is fine.

Well, yes and no. Calculators help. Especially with complex numbers. But calculators are worthless if you don't know what you are doing. That's why it is good to write things down in an orderly manner. And be particularly careful with your units. Be sure you haven't forgotten an important step.

I lay out the problem as a series of steps, and see if it makes sense. Then I do the calculations. I'll use the previous problem as an example. (This is MY way of doing the same problem. That's not to say that you did it wrong because you did it differently.)
First I ask myself, "What do I have?" ("What do I know?") and "What do I want?" ("What do I want to know?").

That's right. The next step is to recognize the connection between what I "want" and what I "have". In this problem it is the units of specific activity that makes the connection.

Well the units of specific activity are "Curies per gram". Right?

And a Curie is 37 billion disintegrations per second. Another way of saying that is, 1 Curie EQUALS 37 billion disintegrations per second.

Good. Now I line the units up in order to go from what I have to what I want.
The rock is 100 grams and produces 370 billion disintegrations per second.
I'm going to write that as "370 bdps/100 grams".

Yes it is. But let's not move too quickly. Let's also remember the units we want to have at the end of it all. We want the answer to be in Curies per gram, because that's what specific activity is! So we must "convert" disintegrations per second into Curies.
Conversions are a very important part of science math problems. Some people panic when they see "conversion problems". They really don't need to panic. Besides, the panic just makes things worse! If they think about the units involved in any conversion, it all goes very smoothly and clearly.

Well, one Curie equals 37 bdps. I'm going to write that as "37 bdps = 1 Curie". If you have been following my thinking you can now line up my "thoughts" into a single math statement. Try it.

Very good. Now line them up in such as way as to get rid of the numbers and units I don't need while keeping the ones I want.

By converting them. I do that by remembering that any number divided by itself is 1. Also I remember that any number multiplied by one is unchanged. Those two rules are the most important rules in mathematics!

Not useless. Useful! You'll see why in a moment. Now, have you thought that 37 billion disintegrations divided by a second equals one?

37 billion disintegrations divided by one second equals one. One Curie! Remember?

So, one equals 1 Curie divided by 37 billion disintegrations per second.
That's written as "1 = 1 Curie/37 bdps".

Yes. Exactly. Now, let's get back to the problem.
That 100 gram rock produces 370 billion disintegrations per second.
And, "1 = 1 Curie/37 billion disintegrations per second".
Now, what would happen if I multiplied the 370 billion disintegrations per second in that 100 gram rock, by 1?

Yes you are right. It "does nothing" and it is unchanged. But we can do something and change the number if, instead of multiplying by one, we multiple by "1 Curie/37 bdps". When we do that we are just multiplying by one because "1 = 1 Curie/37 billion disintegrations per second". That's the same as 1, but it allows us to convert our problem into the units we want.

That's right. Now let's write this all out as an "equation".
370 bdps/100 grams (that's the rock)
multiplied by
1 Curie/37 bdps.

Yes. And now you have your answer!

Let's write it as a proper math expression. It will make it more obvious.

Notice that the bdps above and below the fraction line "cancel each other out".

Yes you could have. And the bdps disappears because you are dividing something by itself (bdps/bdps =1). That leaves you with just a clean "10".

Oh, yes. We divide that 10 from above, by the 100 grams of rock to give 0.1 Curies/gram. And that is our answer. The specific activity is 0.1 Curies/gram.

Well, it is a disciplined way to do the problem. And it works for me! It lets me keep track of the units and lays it all out in a clear manner.

No. If you have a way that works for you and you are happy with it, then stick with it. However, I've found that by lining up all the information, and juggling the math around to reflect what I am trying to get at, I arrive at the right answer every time.
And speaking of time, I think it is time to end this lesson. Any final questions about atoms?

Yeah. Where did atoms come from? How were they made?

Oh, goodness! You do like to tackle the big questions don't you?
The universe and everything in it started many billions of years ago in a Big Bang!

Yes. But not your typical explosion. It was an explosion from nothing that created everything.

Yes, it does. It isn't quite magic, but it is about as close as science gets to magic! And I assure you it isn't nonsense either. I don't want to get into the details of exactly how this Big Bang came about. It's a very specialized subject and I'm not sure I fully understand it myself! Suffice it to say that out of this huge explosion came all the protons, neutrons and electrons which make atoms.

No, just the smallest and simplest elements were made directly from the Big Bang. The vast majority of atoms created were just hydrogen and helium, with all their various isotopes. That's why they are so common.

Yes. But there was also a trace of the next heavier elements: lithium, beryllium and boron.

It's very simple really. These next three elements were the ones to have more protons (and neutrons and electrons).
Lithium has 3 protons and is abbreviated (Li).
Beryllium has an atomic number of 4 and is abbreviated (Be)
And boron has 5 protons and is written as simply (B)

Well lithium usually has 4 neutrons.

Yes. Most lithium, but not all lithium, has 4 neutrons, which along with the 3 protons (which define it as lithium) give it an atomic mass of 7 Daltons. However, some lithium has only 3 neutrons.
But, see here, I don't want you to try to memorize ALL the various isotopes. It's good to know the isotopes of hydrogen and a few special isotopes. But it will be a waste of your time to memorize them all. You can always look up their atomic mass later. If you need to. No Alchemist goes far without his "Handbook of Chemistry". Recall, it is the number of PROTONS that really matter.

Yes, that's right. Also, some were made in a process called "nuclear synthesis" which means the creation of nuclei.

With the starting material of the Big Bang - the hydrogen and helium mostly. And the "how" was (and still is) "nuclear fusion"

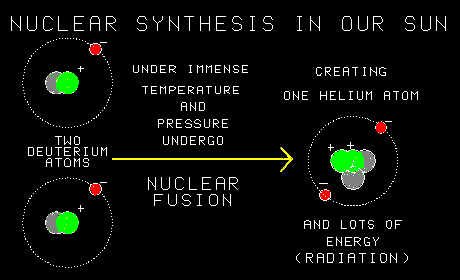
As the name implies, nuclear fusion is a reaction in which the nucleus of one atom fuses with the nucleus of another. I see. And by adding together two atoms, you add together all the protons that were in them. So you build heavier elements using the light ones. Yes. Exactly. In the process you also make an awful lot of energy. Lots of gamma rays! Sounds dangerous. And this still goes on? Inside stars?

Yes indeed. The main nuclear fusion reaction is the fusing together of two hydrogen atoms to get helium. The leftover energy powers the sun! And most of the other stars in the universe too.

Yes, and the universe is making more helium as it powers the sun and stars. But I see you are getting anxious to learn how the heavier elements were formed.

That's right. As a star grows old it uses up its hydrogen. Eventually there is nothing but helium in the star. Then the star shrinks and starts to slam the heliums together...

Yes, but I haven't finished my story. Two berylliums can get slammed together to make an element with 8 protons, oxygen. Oxygen makes up about 20% of our atmosphere.

Yeap. And so were most of the atoms in your body. The carbon atoms, with 6 protons are the result of fusing other smaller atoms.

Right. The exact nuclear reactions are not important for us to go into. But, as you can see, it is simply a matter of slamming atoms together, fusing their nuclei, and getting new elements. There are also a lot of unstable nuclei formed and they rapidly decay into more stable forms, giving off all three forms of radiation as they rearrange their new nuclei.

Yes, it is. These nuclear fusions go on all the time inside stars all over the universe. Eventually they end up with atoms containing 26 protons (and a bunch of neutrons). We call that element iron.

No. Iron is the heaviest element created within stars. But after a big star has "burned" all its nuclear fuel and run out of options, it undergoes a final big squeeze and then explodes!

Yes. We call it a "nova". During this tremendous explosion, more atoms are slammed together and elements heavier than iron are formed. Like cobalt, mercury and gold!

Don't worry. This star will not die for billions of more years.

That's right. The iron in your blade and in your blood was once at the center of a star, billions of years ago. So was the air we breath and the water we drink.

You said it. I think that is really amazing, don't you?

Why not take a break and think about that? After you've had a rest we'll go into the most important part of Alchemy and atoms.

Well, that's an over simplification. Electrons are the part of the atom involved in all the Alchemy!

That's right. The protons define the element because they determine how many electrons are around the nucleus. But the electrons do all the work in Alchemy.

Right.

Good questions. The number of protons defines the element ...

The number of electrons determines the Alchemy. Even ions, with their unbalanced load of electrons, will have a chemistry based on the electrons. BUT, and it's an important "but", the Alchemy of ions is really influenced by the fact that the ions are unnaturally unbalanced.
I'm getting ahead of myself here. We'll come back to that in the next Ancient Element, WATER.

What?

Why, yes. That's a good way to think about it.
Anyway, let's move on. I think you should learn about the electrons with as much detail and determination as you have used for learning about the nucleus. Perhaps more! This next section about electrons isn't easy but it's important to learn ...

Stop that!

I can still hear you.

Well, the electrons which surround the nucleus of each atom are arranged in very specific ways. Those specific ways determine how the atom will react with other atoms. And that's what Alchemy is all about, isn't it? Atoms reacting with atoms?

No, no. Goodness no! The nucleus of the atom is very important because it defines the number of electrons and their behavior!

The first "trick" to electrons is to understand electron shells.

No. No. Like egg shells or something like that. Think about layers when you think about electron shells. And think back to what you know about electrons.

When you say they "circle the atom" you may be misleading yourself. The electrons are actually whizzing around the atom in patterns that would make a sphere or other three dimensional pattern, not a circle. The rest of this Ancient Element will teach you exactly how they are moving around the nucleus and the shapes their orbits make.

Right! We Alchemists like to say electrons move around the atoms in "shells". We often draw those shells to look like circles, but shells don't have a shape. Shells are just an energy level for the electron to sit in. I suppose you can think of them as the size of an atom because the outer most shell determines the atom's size. But not its shape.

That would be the orbitals. That's the second level to understanding electrons. But I'm getting ahead of myself. Lets' deal with shells first.
Now tell me, what else do you recall about electrons and protons?

Yes. Exactly. So a hydrogen atom must have one electron in its shell, in order to neutralize the proton's positive charge.
Oxygen has 8 protons,...

Yes.
Actually, oxygen can't cram 8 electrons into one shell. It splits them up into two different shells.
The first shell, the shell closest to an atom, is called the K-shell.

No. "K" is for no reason at all, as far as I know. But at least I know how to spell!
Anyway, the K-shell is a small shell and can only hold two electrons. For hydrogen or helium that's all the shell room you need. So hydrogen and helium only have a K-shell.

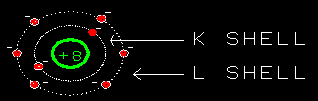
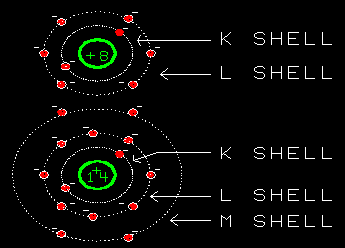
Yes, they do. Just outside the K-shell is the L-shell. It can hold another 8 electrons. So oxygen's six remaining electrons go into the L-shell. (I'm going to start drawing the nucleus as just a circle with a charge, leaving out all the individual neutrons and protons.)

Hey, if 8 electrons can fit in the L-shell, why don't all 8 of the electrons go there? You know, be all together. Friends! I would. Why don't the electrons?

Because they behave like electrons not like you! Electrons fill shells in a very precise way defined by physics.
Electrons are attracted to the proton by its opposite charge. Opposite charges attract. So two "lucky" electrons get closer to the protons by taking up positions in the K-shell, leaving their "friends" behind.

Quantum mechanics.

Not who. What? Quantum mechanics rules the world of the very small. In 1912 a young Danish physicist named Niels Bohr explained that electrons can be in shells (or "orbits") only at well-specified distances from the nucleus. These specific distances are the shells. They are explained by quantum mechanics. Also, the shape of the orbits (orbitals), the number of electrons they can hold, and how the electrons behave, are all explained by the rules of quantum mechanics.

No. Not at all. Quantum mechanics sets the rules of chemistry, but you don't need detailed knowledge of quantum mechanics. All you need to understand is that quantum mechanics sets the rules. Know the rules but don't worry about the details from which they came.
It is convenient to imagine the electrons as having certain "likes and dislikes", the way a person likes or dislikes something. But quantum mechanics is the real reason behind electron behavior.

Right. Shells have to do with the energy of the electrons and they determine the size of an atom, by determining the distance the electrons are from the nucleus.

I see. The electron shells of oxygen are arranged with 2 electrons in the K-shell and 6 in the L-shell. With room for two more. Yes, exactly. And that "room for two more" is very important, as you will see when we talk about bonding and molecules in the next Ancient Element, WATER. But let's stick with atoms. Bigger atoms have more shells to juggle more electrons. Silicon has 14 electrons to arrange in shells, so it has to place the last four into the next largest shell. Guess what that shell is called. The M-shell?

Yes. Simple isn't it? As the atoms get bigger we add on more shells to accommodate their electrons and move up the alphabet as we name each new shell.

Fortunately, atoms don't get so big that we need that many shells.
You should remember that each shell is bigger than the one inside it, so it can hold more electrons.

The M-shell can hold up to 18 electrons. The N-shell can hold another 32 electrons.

Yes, it would be.

Right. That is good enough for our purposes. It works well for all the small elements and those are the ones that make up most of Alchemy.

With some of the larger atoms, those with lots of electrons, peculiar things happen with the filling up of the shells. It has to do with some extra complexities about electron behavior.

Yes, but we don't need to go into that now.

I want to learn about the shapes of atoms. Are atoms round? Like a sphere? Like tiny balls?

Some are and some aren't. It depends on what element that atom is. And it depends on what you call a sphere.

Well, it's easy to fall into the habit of imagining atoms as tiny spheres. But atoms are not tiny balls of matter, even though we often think of them that way.
Tell me Arthur, how would you describe the shape of hydrogen or helium atoms?

Sort of right. It is fair to think of the nucleus of an atom as a sphere or a group of spheres (made of protons and neutrons). But atoms are more than a nucleus.

Right. And I'm glad you said "orbiting" instead of "circling" (that time). Even I fall into the habit of saying the "electrons circle the nucleus". That implies the electrons move around the nucleus the way the moon circles the earth.

No, they don't. This brings us to the edge of the "magical" world of quantum mechanics.

Don't worry. We won't go too deep. The important thing to understand is that an electron orbiting a nucleus is not following a set path around it. Instead it kind of winks in and out of positions all around the nucleus.

Electrons are very small. They are at the very limits of "reality". The world of the very small is dominated by a curious kind of existence based upon statistics and probabilities.

It is! There is nothing in our normal (big) world that compares to it.

Well, let's define the shape of an atom as the shape of its electrons' orbits. OK?

Good point. Imagine a hydrogen atom with its one electron. How do you think the hydrogen could appear as a sphere?

Yes, I do. You are right to point that out. You see, the moon circles the earth along a single plane. Even if it were to move very fast, it would not form a sphere around the earth.

Right. The moon-earth system is shaped like a ring. Not a sphere. But an electron orbiting a nucleus does not form a ring around the nucleus. It makes a sphere. It is a common mistake to think that electrons orbit the nucleus in flat planes. They don't.

Right! And that is exactly what happens around hydrogen. The electron makes a sphere around the proton (and any neutrons) by moving incredibly fast. At any particular moment the electron is in a certain position but it moves so quickly that it is impossible to say "Oh, the electron is right here."

Yes! (Also there are other reasons why it is difficult to define the position of an electron but that's an advanced topic.) Therefore, Alchemists picture the electron as being somewhere around the nucleus, but they can't say exactly where.

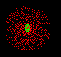
Right. BUT there is a certain probability that it is within a certain volume around the nucleus. We call this volume the electron cloud. Here's a drawing of a hydrogen atom's cloud. Each red dot represents the electron at one point in time. It is NOT to mean the atom has hundreds of electrons. It just has one electron that moves so much that it forms a cloud.

I see. Is it this electron cloud which determines the shape of an atom?

Yes.

No.

Remember, those were shells and shells are not meant to represent the shape of the atom. Shells represent the energy levels and size (radius) of an atom.
The time has come to introduce the idea of subshells, which are also called "orbitals". They cause shape. Bohr thought all atoms had sphere-shaped electron clouds, like hydrogen. He was wrong. He didn't know about subshells.

No. Those shells are the principle shells. Those principle shells have subshells to them. Subshells are a detail of shells.

We are, so pay attention. The shells (K, L, M and so on) are a convenient way to imagine electron clouds. They define how far away the electrons (in that shell) are from the nucleus.
Shells have to do with atomic RADIUS.
But when you start to look at shells in detail you learn they are made of subshells which we call "orbitals".
Orbitals define the true SHAPE of the electron cloud and thus the true shape of atoms.

Right!

Right.
There are 4 basic subshells, or orbitals, each with a specific shape - s orbitals, p orbitals, d orbitals and f orbitals. The easiest subshell to understand is the s orbital. Electrons in an s orbital are a specific distance from the nucleus (determined by the shell), but can be in any direction around it.

It means that electrons in s orbitals form an electron cloud shaped like a sphere.

That's easy! S orbitals are spheres. Right. Their electrons are likely to be found in any direction from the nucleus (that's a characteristic of an s orbital) so that makes a sphere. Those electrons are at a certain distance from the nucleus (that's a characteristic of their shell). Hydrogen and helium have only s orbitals, so hydrogen and helium are simple spheres. The fact that they have only K-shells means they are (roughly) the same size. Aren't they the only elements with K-shells as their outer (only) shell?

That's right. As a matter of fact, K-shells can ONLY have s orbitals.

Yes. In fact, ALL shells have s orbitals.
L-shells have s orbitals and they also can have p orbitals.

P orbitals are shaped like a pair of lobes. Like a figure 8. But not a flat figure 8. It's like a figure 8 that has been spun in the 3rd dimension (out of the page).

OK, lets' back up a wee bit. Imagine the letter O, written on a page. It has the shape of a plate, a disk. But the s orbital is NOT a disk, it is a sphere. You can imagine that the "O" is spun in the 3rd dimension (out of the page) to make the sphere.

Good. To understand the shape of p orbitals, imagine the figure 8 is spun the same way (along its long axis). It makes a pair of lobes.

If you think it's making a doughnut shape you are imagining it spinning along the short axis, not the long axis.

OK, try this. Imagine the figure 8 to be dangling from a string. If you give it a spin, it will look like a fat figure 8 made of two lobes. One lobe at the top and another at the bottom.

Right. The center of the figure 8 is at the center of the atom. At the nucleus.

Aye. The p orbitals are more complex than s orbitals because they can have three different orientations. That means there can be up to three different types of p orbitals.

It is!

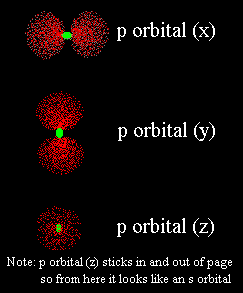
What is it? "Orientations"? What's that all about? What I mean is the figure 8 could be positioned in any one of the three dimensions. What are the three dimensions? Well, some people think of the three dimensions as "height, length and width". That's pretty good, but we Alchemists (and other scientists) call them "x, y and z". It has to do with a form of math called geometry. Ugh. Not math! Don't worry about it. Just imagine three different figure 8 lobes lined up in the three directions. One lies up and down (like the 8), another points sideways (left and right) and the third points in and out of your book.

Well, actually it has to do with quantum mechanics. But your guess is pretty close to the truth and good enough for our class. The smallest atoms have only a K-shell so all they can have is a simple s orbital. A sphere. But bigger atoms can also have p orbitals.

Yes. All together there are four kinds of orbitals - s, p, d and f.

My, my you ARE an inquisitive lad. There are 5 different types of d orbitals and 7 different types of f orbitals. Each type is a complex mix of spheres, lobes, rings and other strange shapes. They make the p orbitals look easy!

Not from me. Not in this class. Fortunately, those complex orbitals are only found in certain metals. Only advanced Alchemists bother to learn about d and f orbitals. Most of the elements you are likely to work with have only s and p orbitals. Or combinations of s and p orbitals.

Yes, it is. Let's take oxygen as an example. First, remind me how the electrons are arranged in oxygen's shells.

Yes! That's right. All atoms have K-shells, so all atoms have a sphere (s orbital) as the inner most orbital. But it's the orbitals in the OUTER shell that give an atom its shape.

That's right. And this is where many Alchemy students get confused. Remember, there are TWO groups of orbitals in the L-shell. There is one s orbital (only one type) and one group of p orbitals (of three types: x, y or z).

Well, the electrons are distributed from the lowest to the highest energies.
All elements fill their s orbitals before they fill their p orbitals because s orbitals are lower in energy than p orbitals. It's another law. It's just like filling the K-shell before moving on to fill the L-shell. But here we are talking about orbitals. S orbitals are of lower energy than p orbitals so they get filled first.

No, that would be wrong. But you wouldn't have known that until you learned about Pauli's exclusion principle.

Pauli's exclusion principle tells us that no more than two electrons may occupy a single orbital. (Pauli's exclusion principle also says something else, but we'll leave that for later.)

Aye. Quantum mechanics determines all these rules about the way electrons behave. With the K-shell, you only had a single orbital, so both electrons fit in it without difficulty. But now we have more electrons to juggle in the L-shell.

Yes. We are getting into the details of atomic structure. It's called "electron configuration".
The K-shell can only hold two electrons because it has only an s orbital.
The other 6 electrons that go into oxygen's L-shell are distributed among the s and p orbitals. And remember, there are three different types of p orbitals - x, y and z.

Now, come on Arthur! Don't let that get you down. You learned how to fill shells in a specific order. All you are learning now is how to fill the orbitals in specific order. Now tell me how you would distribute the remaining 6 electrons in oxygen's L-shell. Remember, the s orbital is of lower energy than the p orbitals so it will get filled first.

Right. That takes care of 4 of oxygen's electrons. Two are in the K-shell (which only has a single s orbital) and two more are in the s orbital of the L-shell.
And that reminds me of an interesting point worth repeating. Because there is only one type of s orbital and orbitals can only hold two electrons, that means all s orbitals can only hold 2 electrons. And all shells start with an s orbital (as the lowest energy of the shell).

No, sorry if I have. What I am trying to point out is that the s orbitals are found in all shells - K, L, M, and so on. But the s orbitals are only of one type. You can only have one type of sphere. There is no other kind.

My point is that p orbitals, which are of higher energy than s orbitals, are in THREE types (x, y, and z). So p orbitals are where you spend most of your time figuring out the patterns. P orbitals are more complex than s orbitals.

Right. Now let's get back to the oxygen problem. You have 2 electrons in its K-shell (s orbital) and 2 electrons in the L-shell's s orbital. That leaves you with four electrons remaining.

Sort of right. This brings us to another rule about electron distribution.
Hund's rule says that when more than one orbital is available for occupation, electrons occupy separate orbitals first. (Hund's rule also says something else, but we'll leave that for later.)

So, assign one electron to each p orbital.

It goes into which ever p orbital you want to put it.

Well, you might think to put one electron in the x type and one in the y type and the other two in the z type.

Of course he's happy. Think about it. All Hund says is that you must first put an electron into each orbital (of the same energy level, of the same shape). Once all the orbitals (of the same energy level of that shape) have an electron, you can start placing the other electrons into orbitals to create orbital electron pairs.

Right. It doesn't matter which p orbital (x, y or z) ends up with a pair of electrons. All that matters is that first all the p orbitals get an electron. The first three electrons will go into the three p orbitals, one in each.

Yes, that's wrong. Pauli would be pleased (because there's no more than two electrons per orbital) but Hund would not be happy (because Hund wants all the orbitals of the same energy to get an electron before doubling them up in pairs).

Yes, I agree. But these rules are the rules of quantum mechanics.
You could have ended up with two electrons into the z-p orbital and one electron each into the x-p and y-p orbitals. That would have been correct too. It's all the same. It doesn't matter because all the p orbitals in the same shell have the same energy.

Right. The s orbital is the lowest energy orbital of any shell, so it is the first to be filled. Once you have two electrons in it, you must move up to the three p orbitals to distribute the rest.

Right. That's because all three of the p orbitals are of the same energy. They are identical, so we use Hund's rule to distribute electrons among orbitals of the same energy. The three p orbitals (x-p, y-p and z-p) are identical in energy (they are only different in orientation).

Correct! We could summarize the orbitals of an oxygen atom by writing it down like this.
Oxygen's K-shell (s²)
Oxygen's L-shell (s², x-p², y-p¹, z-p¹)

Yes, I agree. There are other ways to write the same thing. But this way is a good way. Regardless of how you write it, you should understand how you figure it out!
Just remember to:
1) fill all shells first, starting with the lowest energy shell (K) and working outward (L, M, etc.).
2) then re-assign electrons starting with the lowest energy orbital (s orbital) and then moving up to the higher energy orbitals (the p orbitals).

Right.
Now remember, the reason we went through all this hard work is we wanted to know the SHAPE of the oxygen atom.

Right, you are. You can ignore oxygen's s orbital in the K-shell. It's hidden underneath the L-shell. In order to "see" the shape of the oxygen, you must overlap the shapes of all its L-shell orbitals.

Just line them up and overlap them. Remember, the nucleus is at the center of ALL orbitals, so you can imagine laying one electron cloud from each orbital over the nucleus. When all the outer shell orbitals are overlapped, you get the complete shape of the atom! I think I see what you mean. I also see that the x-p orbital is full so it is twice as thick as the other two. Right, and that's an important point. Just because an orbital is only half-full, that DOESN'T mean the electron stays in just one lobe. It moves between the two lobes equally. Half-full orbitals are just less dense. I get it. When I overlap all of oxygen's L-shell orbitals I see a thick sphere in the center (the s orbital), a thick pair of lobes (the full x-p orbital) and another two pairs of lobes which are less thick. They are at right angles to the thick one. Yes, you've got it. Naturally it's hard to draw it well in only two dimensions, but I think you can imagine its shape.

Yes. It's those p orbitals. They really spice things up.
Remember, I could have ended up with that electron pair in a different p orbital and it would still have been correct. Why not write that for me? Show me how to write the electron structure of oxygen with the electron pair in a different orbital.

Correct. Notice that the atom will still have the same shape, it will just be in a different orientation.
All atoms work that way. But there's two things I want to point out.
First, in some of the large metal atoms, the d and f orbitals must be included in the puzzle. Their orbitals are in odd shapes and there are more types of them (5 of the d types and 7 of the f types).
Second, in some larger atoms (with lots of electrons) the energy levels of the orbitals from different shells start to overlap. That causes some electrons to be in a larger shell and in a different orbital than you might expect.

Yes, there are. Even these "exceptions" can be understood if we went into the details of assigning electrons to their orbitals. But in this course, at this level of your education, I want to stick to small atoms and simple rules.

Well, they are understandable. The complexities I want to avoid here, have to do with the details of electron energy levels in big atoms.
Regardless, ALL orbitals must obey Pauli's exclusion principle and Hund's rule. Even the d and f orbitals. Even the big atoms.

Well, they aren't really all that hard. They follow the same rules. But their shapes are hard to imagine and I'd have to teach you a more difficult way to figure out how the energy levels of each atom are determined. You see, the bigger shells have d and f orbitals, but they don't like to use them. That causes electrons to skip up to higher shells and I don't want to go into that here.

We won't. Besides, you won't miss much by not doing them. Maybe some other day.

However, it is important to understand the s and p orbitals, so let's do another atom.

Arthur! I'm surprised at you.

That's all the more reason to practice on another element. I'll help you as you go.
Try to figure out the electron structure of carbon.

Well, it has 6 protons ...

Right. Always start with the shells. The shells are the principle electron configuration and they help you figure out the size of the atom's electron cloud, but they don't tell you the shape.

Right.

Nope. You got it wrong.

Calm down. You've made a common error. Remember that s orbitals are of lower energy than p orbitals. So the s orbital gets filled first. Filled completely with both electrons.

They do. And you're right, it is tricky. The difference in energy between an s and a p orbital is very small. Much smaller than the difference in energy between a K-shell and an L-shell. But there is a difference. S orbitals are of slightly lower energy than p orbitals, so they are filled first, completely, with two electrons.

What do you think you should do? Remember, all you have to worry about is Hund's rule.

Is that a problem? Are you breaking any rules by leaving an orbital empty?

It may feel wrong, but it is right! There's nothing wrong with leaving an orbital empty if that's the only way to finish the atom. So tell me, what's the electronic configuration of carbon?

That's right, although we usually don't bother writing the empty orbital. Any good Alchemist would know it should be there and know that it is empty.

Did it matter with the oxygen's p orbitals which one got the pair?

Right.

Right. They are all right. All three ways of assigning them are right for two reasons. First, we can't tell the three orbitals apart, and second, the electrons can't tell them apart either! As a matter of fact the two electrons in the p orbitals of carbon's L-shell probably move all around to form all three possibilities.

Well, the two electrons in the p orbitals have the exact same energy so they can end up in any one of the three orbitals at any one time. The only thing they can't do is ...

Right you are! You can't have an orbital with a (x-p²), (y-p²) or (z-p²) because that would disobey Hund's rule.

Right! Now, can you imagine the final shape of a carbon atom?

Right again. One of the p orbitals is missing, so the carbon atom is kind of flat looking.
I won't bother drawing it because you should try to imagine them yourself. We can only draw in two dimensions but we can think in all three dimensions, so it's good to practice using your imagination to "see" the shapes of atoms.

That's an excellent idea.
Nobody understands how to assign electrons to orbitals the first time they see it. You have to go through it a few times and practice it. Think of these as puzzles to be solved rather than simply questions to be answered.

Yes, I agree.
It's also a good idea to exercise your "visual imagination". Some people think that only artist use their "mind's eye", but Alchemists do it all the time.

It is.
Any questions?

Yeah, but I think I might regret it. You said something about Pauli's exclusion principle and Hund's rule that made me think there was one final layer of complexity. You said they say something else but you'd talk about it later.

Oh, yes! Spin.

Yes. Sort of. All electrons have a final property that I forgot to mention called spin. It is the last part of quantum mechanics, but it ties in to all the rules.

Not really. Not as hard as this other stuff.

Spin isn't like the spin of a top, but some Alchemists like to think of it that way. Spin is the way an electron can "be". Rather than go into the details, let's accept that an electron can be in two different states.

Yes. It doesn't matter what you want to call them. Just so long as you know that they are opposites of each other.

Unfortunately, some Alchemists call them +1/2 and -1/2. But they have nothing to do with their charge. (Remember all electrons are -1 in charge.)

Because they are defined by a "wave function" in math and I won't go into it at all. It requires a great deal of math called trigonometry. All you need to know about spin is that there are two types and they are opposite to each other. Most Alchemist prefer to call them "up" or "down". I like that because it avoids that confusing half numbers of trigonometry.

It helps refine our understanding of electron configurations and helps explain some pretty advanced Alchemy involving weird bonds, magnetism and stuff like that. But that's far too advanced for us here.

Oh, that. Well, Hund's complete rule is that when more than one orbital is available for occupation, electrons occupy separate orbitals ...

... and do so with parallel spins.

There's little reason why you would have to know that for a course at this level. But you asked!

Yes, that's exactly what Hund's rule would say.

That's right!

You tell me. Think about Hund's rule, now with his spin rule.

Absolutely right. What about that last electron? It has to pair up with one of the three. What do you think its spin will be?

That's a good guess, but the wrong one. You wouldn't have know that. You see Pauli's exclusion principle says that no more than two electrons can occupy a single orbital ...

... and if two electrons do occupy a single orbital, their spins must be opposite.

Yes! Exactly! And congratulations are in order here.
Arthur, you now understand the most important details of atomic structure AND quantum mechanics!

That's right!
Very advanced Alchemists will understand quantum mechanics using math instead of they way we've done it, but all this talk about electrons has taught you all four levels of quantum mechanics.

OK, let me explain.
The first level of quantum mechanics are the shells. K-shells, L-shells, etc. are the first quantum level.

That would be the subshells or orbitals. You know all four kinds of orbitals: s, p, d and f orbitals.

True, but that's all you really need to know (for most Alchemy). And those "types" of orbitals are the third level of quantum mechanics. The third level of quantum mechanics involves the orientation of the orbitals. You know that there is only one kind of s orbital and it's shaped like a sphere

Right. That's all there is to the third level of quantum mechanics!

Right! That's the four levels of quantum mechanics.

Well, yeah they are. I want to avoid the math that separates them.

That's right. When you know all four quantum levels of an electron, you know everything about its home in an atom. You know what shell it's in, you know its orbital shape and type, and you know its spin.

That's right! No two electrons can have the exact same values in an atom. That's really what Pauli's exclusion principle is all about.

Right. That is the most important law in quantum mechanics. Pauli says no two electrons can have the same four quantum values. They are excluded from sharing the same values. That's why it's called Pauli's exclusion principle!

Good. Pauli and Hund would be proud. And so am I! You've learned a lot of difficult material here.

Good idea. As you review your electron configurations, think about Pauli's exclusion principle as well as Hund's rule. Once you feel comfortable with all this, read through your notes and then go through the Questions and Answers. Remember, some of the Questions are very hard and teach you new things. So don't feel bad if you don't get every answer right. Just be sure you understand the answers I give for them. Enjoy them as puzzles, OK?

---

The Course

The Syllabus

How can I get a FREE and COMPLETE copy of Principles of Alchemy (Chemistry) for myself?

Frequently Asked Questions

Go to the Homepage

This work was created by Dr Jamie Love and licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.